Class 9 Science Motion
Science Motion Class 9 Notes
| Class | 9th |
| Subject | Science |
| Chapter Name | Motion |
| Medium | English |
Introduction
In everyday life, we see both still and moving things. Birds fly, fish swim, blood flows, and cars drive. Atoms, planets, and galaxies are always moving. We notice movement by position changes or signs like dust and leaves moving. This chapter covers straight and circular motion, including key concepts like distance, displacement, speed, average speed, velocity, average velocity, acceleration, graph of the motion, equation of motion and circular motion.
Motion
A body is said to be in motion if it changes its position with respect to its surroundings.
Rest
A body is said to be at rest if it does not change its position with respect to its surroundings.
Note: Rest and motion are always relative. There is no such thing as absolute rest or absolute motion.
Physical Quantity
The physical quantities that can be measured directly or indirectly are called physical quantities.
Example: Height, Weight, Displacement, Velocity, Acceleration, Force, Length, Time, Speed, Work etc.
Note: Honesty, Happiness etc. are not Physical Quantities.
The physical quantities are divided into two groups: Scalar and Vector
Scalar and Vector
In physics, We deal with various quantities like mass, displacement, velocity, time, acceleration, volume, density, speed, force etc. These quantities are categorized into scalars and vectors.
Scalar Quantities
The physical quantities that can be completely described by its magnitude is called a scalar quantities.
Example: Mass, Length, Time, Speed, Work etc.
Vector Quantities
The physical quantities that can be completely described by its magnitude and direction is called a vector quantities.
Example: Displacement, Velocity, Acceleration, Force etc.
Terms Associated with Motion
- Reference Point: a reference point is a specific location to measure or describe the position or motion of an object.
- Position: position means the location of a certain place or object from a reference point.
- Reference Frame: a reference frame is a coordinate system used to measure and describe the position and motion of objects.
Distance
The actual path length covered by an object is called distance.
- Distance is a scalar quantity.
- S.I. unit of distance is meter (m).
Displacement
The shortest distance between the final position and the initial position of an object in a particular direction is called displacement.
- Displacement is a vector quantity.
- S.I. unit of displacement is meter (m).
Note 1: The magnitude of displacement is always equal to or less than the distance traversed.
Difference Between Distance and Displacement
| Distance | Displacement |
|---|---|
| 1. Distance is the actual path length covered by an object. | 1. Displacement is the shortest distance between the final position and the initial position of an object. |
| 2. It is a scalar quantity. | 2. It is a vector quantity. |
| 3. Distance travelled by a body is always positive. | 3. Displacement of a body may be positive, zero or negative. |
| 4. Distance travelled by a body is always greater or equal to its displacement. | 4. Displacement of a body is always less than or equal to distance travelled by the body. |
Numericals
1. In the following fig , a car moves on the road from the 20 km mark (its initial position) to the 100 km mark. After that,it reverses and moves back to the 50 km mark (its final position). Find the displacement and distance travelled by the car.
Ans. Displacement +30 km, Distance 130 km

2. A ball is thrown vertically upward. It rises upto a height of 10 m, and comes back to the initial position. Calculate: (i) the total distance covered by the ball. (ii) the total displacement of the ball.
3. A boy travels a distance of 10 m towards south, then he turns towards east and travels 12 m in that direction. Calculate: (i) the total distance travelled by the boy and (ii) the displacement from his initial position.
4. A car travels a distance of 15 km towards east, 20 km towards south and then 45 km towards east. Show the motion of the car graphically and determine: (i) the total distance travelled by the car (ii) the displacement of the car.
5. A particle moves in a circle with O as centre and AO = OB = 5 cm, as radius, as shown in the figure. It starts from A. Calculate: (i) the distance covered and (ii) the displacement, when it reaches B.
Uniform Motion
When an object travels equal distances in equal intervals of time, then the motion of the object is called in uniform motion.
Non-uniform motion
When an object travels unequal distances in equal intervals of time then the motion of the object is called in non-uniform motion.
Note 1: When the motion of an object increases with time then it is called accelerated motion.
Note 2: When the motion of an object decreases with time then it is called retarded motion.
Speed
The distance covered by an object in unit time is called speed.
speed=\frac{distance}{time}
v=\frac{s}{t}
- Speed is a scalar quantity.
- S.I. unit of speed is meter per second (ms-1).
Q. Which is the fastest animal on the Earth?
Answer: Falcon, can fly at a speed of 200 km/h
Average Speed
Average speed of a body is the total distance travelled divided by the total time taken to cover that distance.
average\;speed=\frac{total\;distance\; travelled}{total\;time\;taken}
Instantaneous Speed
The speed of an object at the particular time(instant) of observation is known as instantaneous speed of that object.
Speedometer: The instantaneous speed of a vehicle is determined by an instrument called speedometer.
Odometer: The distance traversed by a vehicle is measured by an instrument called odometer.
Velocity
The distance travelled by an object per unit time in a given direction is called velocity.
Or
The rate of change of displacement of an object is called velocity.
velocity=\frac{displacement}{time\;taken}
- Velocity is a vector quantity.
- S.I. unit of velocity is metre per second (m/s).
Note1: The velocity of an object changes due to a change in its speed or its direction or both. Note2: Two moving objects can have the same speed but different velocities.
Instantaneous Velocity
The velocity of an object at any particular instant of time during its motion is called instantaneous velocity.
Uniform Velocity
When a body covers equal distances in equal intervals of time in a particular direction then the object is said to be in uniform velocity.
Non-uniform Velocity
When a body does not cover equal distances in equal intervals of time in a particular direction then the object is said to be in non-uniform velocity.
Average Velocity
The average velocity can be found out by taking the average mean of the initial velocity (u) and final velocity (v) for a given period of time (t).
For uniformly changing velocity
Average\;velocity=\frac{Initial\;velocity+final\;velocity}{2}
Average\;velocity=\frac{u+v}{2}
where, u= initial velocity and v= final velocity
Difference between Speed and Velocity
| Speed | Velocity |
|---|---|
| 1. Speed is the distance covered by an object in unit time. | 1. Velocity is the distance travelled by an object in a particular direction in unit time. |
| 2. Speed is a scalar quantity. | 2. Velocity is a vector quantity. |
| 3. Speed is always positive. | 3. Velocity of an object may be positive, negative or zero. |
| 4. Speed can be equal to velocity or greater than velocity. | 4. Velocity can be equal to speed or lesser than distance. |
| 5. Speed tells how fast a body is moving. | 5. Velocity tells how fast a body is moving along a particular direction. |
Calculation of Average Speed
The average speed of a moving body is calculated by using the following relation.
average\;speed=\frac{total\;distance\; travelled}{total\;time\;taken}Case1: If the distance of total journey is divided into two equal parts with different speeds.
Case2: If time of total journey is divided into two equal halves.
Question: An auto travels at a rate of 25 km/hr for 4 min. then 50 km/hr for 8 min., finally at 20 km/hr for 2 min., find the distance travelled in km and the average speed for complete trip in m/s.
Answer:
Distance travelled = 9 km
Average speed = 10.7 m/s
Acceleration
The rate of change of velocity is called acceleration.
acceleration=\frac{change\;in\;velocity}{time\;taken}
Or a=\frac{v\;-\;u}{t}
- Acceleration is a vector quantity.
- SI unit of acceleration is m/s2
Note: Negative acceleration is also called deceleration or retardation.
Uniform Acceleration
If an object changes its equal velocity in equal intervals of time is called uniform acceleration.
Graphical Analysis of Motion
A graph is a pictorial way of presenting information about the relation between various quantities. The quantities between which a graph is plotted are called the variables. One of the quantities is called the independent quantity and the other quantity, the value of which varies with the independent quantity is called the dependent quantity.
Distance-time Graph
The graph between the distance and time of a moving object at different times is called a distance-time graph.
The change in position of an object over time is expressed by a distance-time graph. In this graph, time is taken along the horizontal axis while the vertical axis shows the distance covered by the object.
Note: The terms distance and displacement are used interchangeably when the motion is in a straight line.
1. Object at Rest
In the graph shown in the following figure, the distance covered by the object with time is zero. That is, the object is at rest. Thus a horizontal line parallel to the time axis on a distance-time graph shows that speed of the object is zero.
Figure
2. Object Moving with Uniform Speed
The speed of an object is said to be uniform if it covers equal distances in equal intervals of time. The distance-time graph as shown in the following figure, is a straight line. Its slope gives the speed of the object.
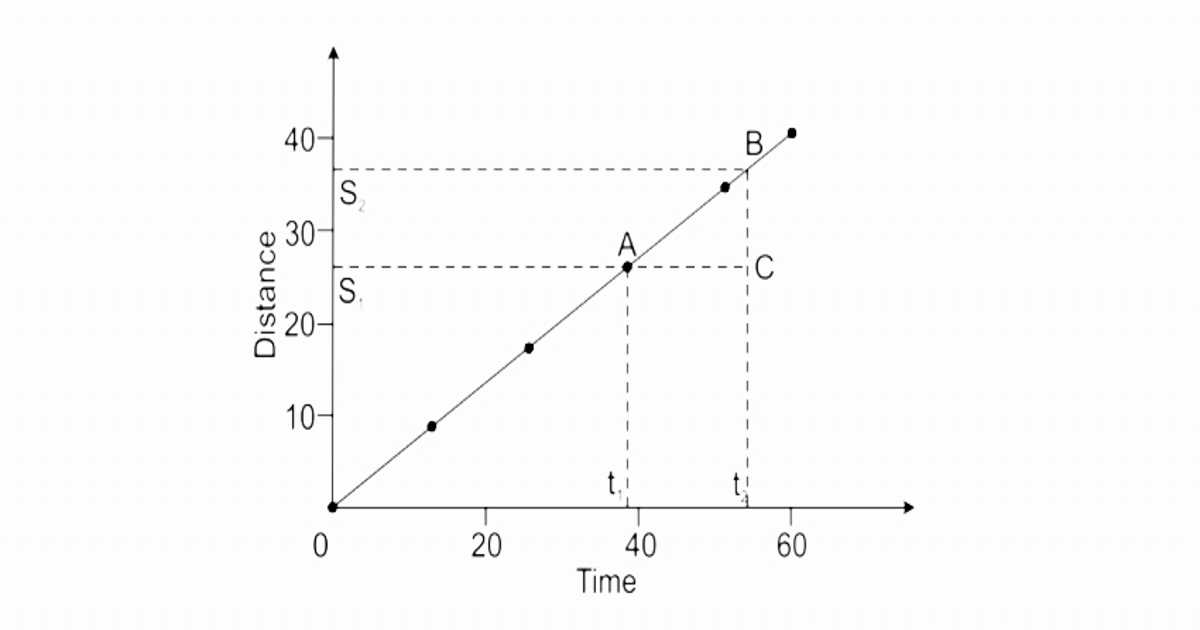
Let s1 and s2 be the distance travelled by the object in time t1 and t2, respectively. Here (s2 – s1) gives the distance travelled by the body in time interval (t2 – t1).
Speed=\frac{Distance\;travelled}{Time\;taken}
Or V=\frac{S_{2}−S_{1}}{t_{2}−t_{1}}
From the above graph:
Speed of the object = Slope of line AB
=\frac{{distance}\;S_{1} S_{2}}{{time}\;t_{1}t_{2}}
=\frac{10\:m}{5\:s}
Speed of the object =2 m/s
The speed found from the graph is 2 m/s.
3. Object Moving with Non-uniform Speed
When an object does not cover equal distances in equal intervals of time then its speed is not uniform. In this case, the distance-time graph is not a straight line as shown in the following figure. The slope of the curve at any point can be found from the slope of the tangent at that point.
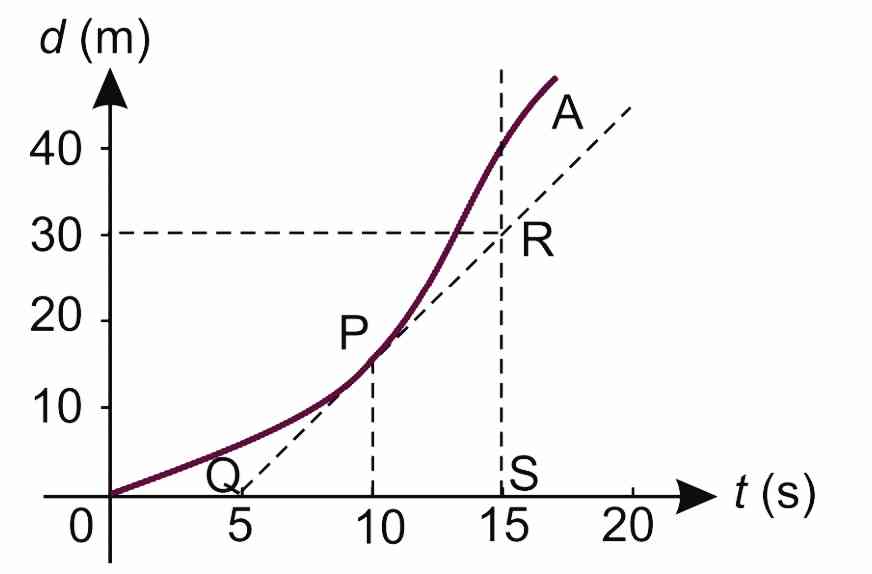
Slope\;of\;the\;tangent\;at\;P=\frac{RS}{QS}
Slope\;of\;the\;tangent\;at\;P=\frac{30\;m}{10\;s} =3 m/s
Thus, speed of the object at P is 3 ms . The speed is
higher at instants when slope is greater; speed is zero at
instants when slope is horizontal.
Velocity-time Graph
The graph between the velocity and time of a moving object at different times is called a velocity-time graph. In this graph, time is displayed on the X-axis and velocity is displayed on the Y-axis.
1. Object Moving with Uniform Velocity
When the velocity of an object is uniform with time, then the velocity-time graph will be a horizontal line parallel to the time-axis along the x-axis as shown in the following figure.
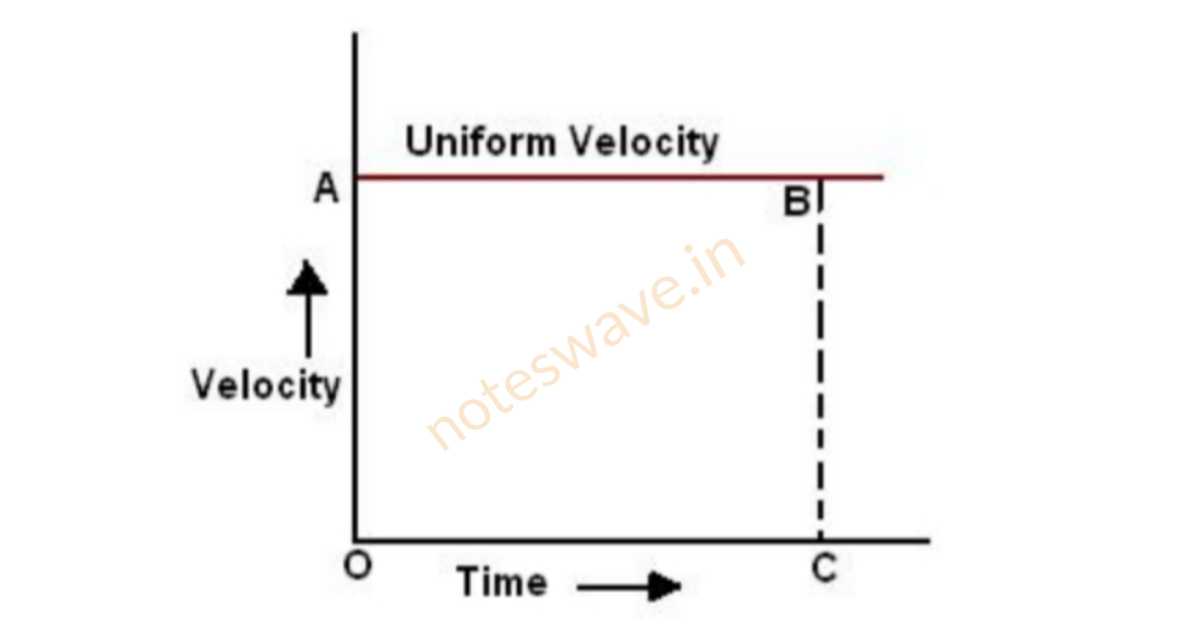
Note: Distance covered by a body is equal to area under speed - time graph.
Note: The distance travelled by a body can also be found from the area under a velocity - time graph if the motion is along a straight line.
Distance/displacement travelled = Speed × Time taken
Distance/displacement travelled = OA × OC= Area of rectangle OABC
2. Object Moving with Non-uniform Velocity (Uniform acceleration)
Let the velocity of an object change uniformly. In such a case velocity is changing at a constant rate. Thus its velocity-time graph would be a straight line as shown in the following figure. A straight line means that the object is moving with uniform acceleration.
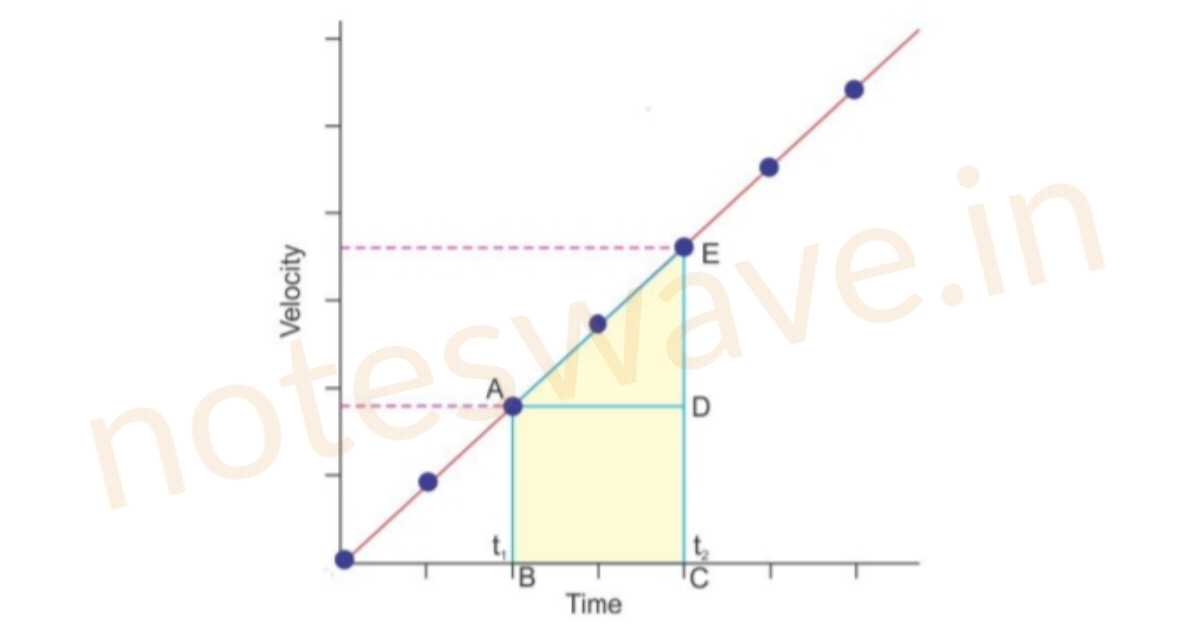
- The slope of the line of the velocity-time graph gives the magnitude of the acceleration of the body.
acceleration=slope\:of\:AE
acceleration=\frac{change\;in\;velocity}{time\;interval}
Or acceleration=\frac{ED}{AD}
- The area enclosed by the velocity-time graph and the time axis gives the distance travelled by the object.
Distance travelled=Area of ABCDE
Distance travelled = Area of triangle ADE + Are of triangle ABCD
Distance\;travelled=\frac{1}{2}×AD×DE+AB+BC
3. Object Moving with Non-uniform Velocity (Non-uniform acceleration)
When there is non-uniform acceleration in the motion of an object, then its velocity changes irregularly and the velocity-time graph is obtained in the form of a curved line or zigzag line.
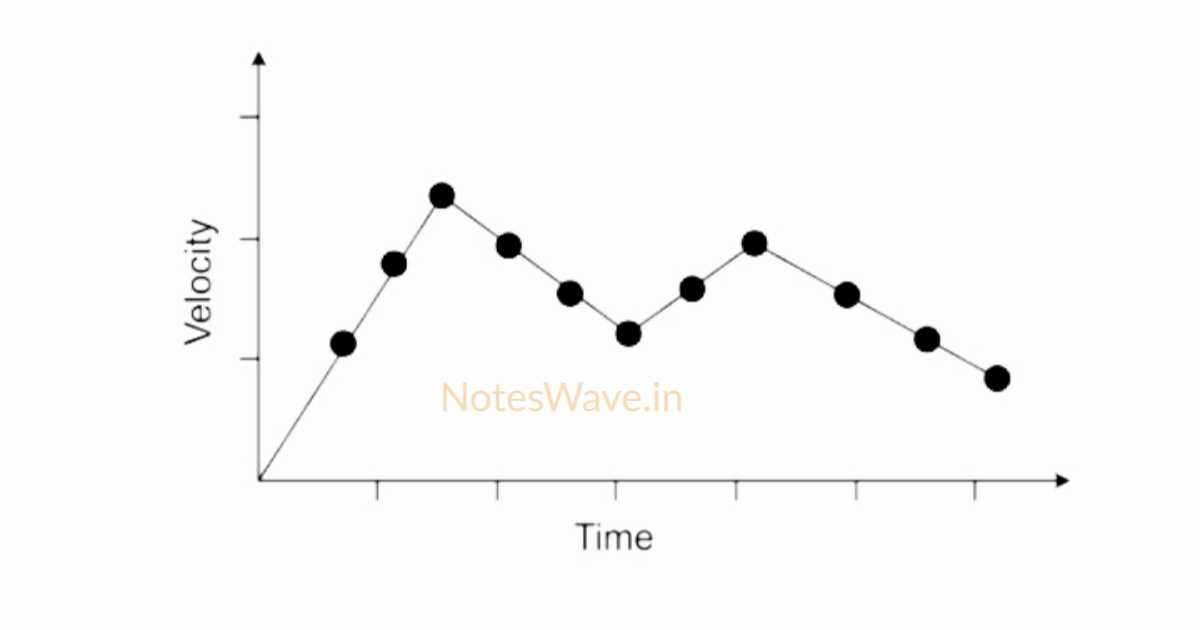
Equations of Motion
There are three basic equations of motion for bodies moving with uniform acceleration. These equations relate initial velocity, final velocity, acceleration, time and distance covered by a moving body. To simplify the derivation of these equations, we assume that the motion is along a straight line. Hence, we consider only the magnitude of displacements, velocities, and acceleration.
The three equations of motion of a body moving along a straight line with uniform acceleration are:
1. v=u+at
2. s=ut+\frac{1}{2}at^{2}
3. v^{2}−u^{2}=2as
where
u -initial velocity
v – final velocity
a – uniform acceleration of the object
t – time taken
s – distance travelled by the object
Derivation of Equations of Motion by Graphical Method
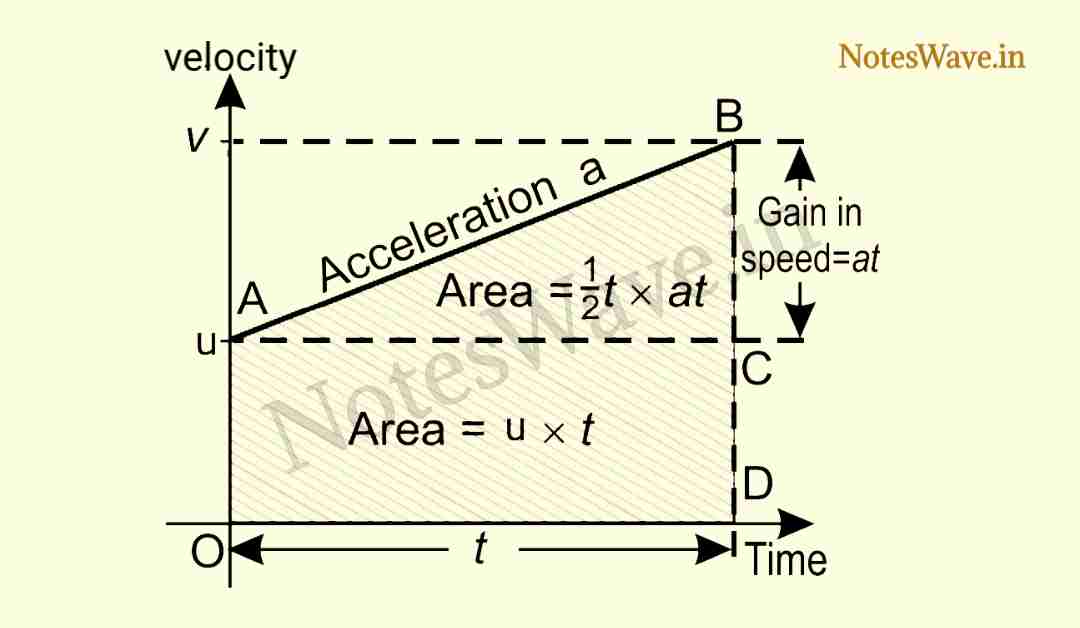
Consider a body moving with initial velocity u in a straight line with uniform acceleration a. Its velocity becomes v after time t. The motion of body is described by speed-time graph as shown in the following figure by line AB. The slope of line AB is acceleration a. The total distance covered by the body is shown by the shaded area under the line AB. Equations of motion can be obtained easily from this graph.
Derivation of First Equation of Motion
Velocity-time graph for the motion of a body is shown in the above figures, Slope of line AB gives the acceleration a of a body.
slop\;of\;line\;AB=acceleration
acceleration =\frac{BC}{AC}=\frac{BD−CD}{OD}
as\;BD=v\;CD=u\;and\;OD=t
hence\;\;\;\;a\;=\frac{v−u}{t}
at=v−u
v=u+at
This is the first equation of motion.
Derivation of Second Equation of Motion
In velocity-time graph shown in the above figure, the total distance s travelled by the body is equal to the total area OABD under the graph. That is
Total distance s = area of (rectangle OACD + triangle ABC)
Area of rectangle OACD = OA×CD = u×t
Area of triangle ABC = 1/2(AC×BC) = 1/2(t×at)
Since total area OABD = area of rectangle OACD + area of triangle ABC
Putting values in the above equation, we get
s=ut+\frac{1}{2}t×at
s=ut+\frac{1}{2}at^{2}
This is the second question of motion.
Derivation of Third Equation of Motion
In velocity-time graph shown in the above figure, the total distance s travelled by the body is given by the total area OABD under the graph.
total\;area\;OABD=\frac{OA+BD}{2}×OD
total\;distance=\frac{OA+BD}{2}×OD
s=\frac{OA+BD}{2}×OD
2s=(OA+BD)OD
Multiply\;both\;sides\;by\;\frac{BC}{OD}
∵\frac{BC}{OD}=a
we get,
2s×\frac{BC}{OD}=(OA+BD)OD×\frac{BC}{OD}
2s×\frac{BC}{OD}=(OA+BD)×BC\;⋅⋅⋅⋅(i)
Putting the values in the above equation (i), we get
2s×a=(u+v)(v−u)
2as=u(v−u)+v(v−u)
2as=uv−u^{2}+v^{2}−uv
2as=v^{2}−u^{2}
v^{2}=u^{2}+ 2as
This is the third equation of motion.
Mathematical Derivation of Equation of Motion
Suppose an object starts moving with velocity ‘u’ and constant acceleration ‘a’ and at instant ‘t’ the velocity of the object becomes ‘v’ and the total distance covered by the object is ‘s’.
Derivation of First Equation of Motion
“Consider a body having initial velocity ‘u’. Suppose it has a uniform acceleration ‘a’ and after time ‘t’ its final velocity becomes ‘v’.
Now we know,
acceleration=\frac{change\;in\;velocity}{time\;taken}
a=\frac{v−u}{t}
at=v−u
v=u+at
This equation is known as the first equation of motion.
Derivation of Second Equation of Motion
s=ut+\frac{1}{2}at^{2} average\;velocity=\frac{u+v}{2} s=\;\lparen\;\frac{u+v}{2\;}\;\rparen\;t s=\;\lparen\;\frac{u+u+at}{2}\;\rparen\;t ∵\;v=u+at s=\;\lparen\;\frac{2u+at}{2}\;\rparen\;t s=\frac{2ut+at^{2}}{2} s=\frac{2ut}{2}+\frac{at^{2}}{2} s=ut+\frac{1}{2}at^{2}
Derivation of Third Equation of Motion
v^{2}−u^{2}=2as
s=ut+\frac{1}{2}at^{2} <br>
v=u+at
at=v−u
t=\frac{v−u}{a}
s=u\;\lparen\;\frac{v−u}{a\;}\;\;\rparen\;+\frac{1}{2}a\;\lparen\;\frac{v−u}{a}\;\rparen\;^{2}
s=\frac{uv−u^{2}}{a}+\frac{a\;\lparen\;v^{2}+u^{2}−2uv\;\rparen\;}{2a^{2}}
s=\frac{uv−u^{2}}{a}+\frac{v^{2}+u^{2}−2uv}{2a}
s=\frac{2uv−2u^{2}+v^{2}+u^{2}−2uv}{2a}
s=\frac{v^{2}−u^{2}}{2a}
2as=v^{2}−u^{2}
v^{2}−u^{2}=2as
v^{2}=u^{2}+ 2as
Motion Under Gravity
Galileo was the first scientist to notice that all the freely falling objects have the same acceleration independent of their masses. He dropped various objects of different masses from the leaning tower of Pisa. He found that all of them reach the ground at the same time.
The acceleration of freely falling bodies is called gravitational acceleration. It is denoted by g. On the surface of the Earth, its value is approximately 10 m/s².
Equation of motion for motion under gravity.
v=u±gt
h=ut±\frac{1}{2}gt^{2}
v^{2}=u^{2}± 2gh
Uniform Circular Motion
When an object moves along a circular path with a uniform speed then the motion of the object is called uniform circular motion.
Note: Uniform circular motion is an accelerated motion because the direction of velocity keeps changing all the time during circular motion.
Examples of Uniform Circular Motion
- Motion of Earth
- Motion of Artificial Satellite
- Motion of Electrons in an Atom
- A spin-drier