Class 10 Physics 2 Marks PYQ Solutions for CBSE 2025 are provided here chapter-wise to help students score full marks in the board exam. All previous year questions are solved in simple language as per the latest CBSE syllabus and marking scheme. These 2 mark questions are important for quick revision before the exam.
Chapter 1. Light: Reflection and Refraction
Mirror
1. During an experiment, a student observes that the given mirror is forming an erect and diminished image for all positions of the object placed in front of it. Based on the this information, answer the following questions
(a) Identify the mirror.
(b) Using new Cartesian sign convention, write the magnitude of the magnification in this case.
(c) What will be the radius of curvature of the mirror if its focal length is 20 cm?
[CBSE 2025]
View Solution
Answer:
(a) Identification of the mirror:
The mirror is a convex mirror, because it always forms an erect and diminished image for all positions of the object.
(b) Magnitude of magnification:
For a convex mirror, the image is always erect and diminished. Therefore, using the new Cartesian sign convention, the magnitude of magnification is less than 1.
|m| < 1
(c) Radius of curvature of the mirror:
Given: Focal length, f = 20 cm
Relation between radius of curvature and focal length:
R = 2f
Substituting the value:
R = 2 × 20 = 40 cm
2. An object is placed at a distance of 30 cm in front of a concave mirror of focal length 20 cm. Use mirror formula to determine the position of the image formed in this case.
[CBSE 2025]
View Solution
Given:
Object distance, u = −30 cm
Focal length of concave mirror, f = −20 cm
Mirror formula:
1/f = 1/v + 1/u
Substituting the values:
1/(−20) = 1/v + 1/(−30)
−1/20 = 1/v − 1/30
1/v = −1/20 + 1/30
Taking LCM (60):
1/v = (−3 + 2)/60
1/v = −1/60
v = −60 cm
Result:
The image is formed at a distance of 60 cm in front of the mirror.
3. An object is placed at a distance of 10 cm in front of a concave mirror of focal length 15 cm. Use mirror formula to determine the position of the image formed by this mirror.
[CBSE 2025]
View Solution
Given:
Object distance, u = −10 cm
Focal length of concave mirror, f = −15 cm
Mirror formula:
1/f = 1/v + 1/u
Substituting the values:
1/(−15) = 1/v + 1/(−10)
−1/15 = 1/v − 1/10
1/v = −1/15 + 1/10
Taking LCM (30):
1/v = (−2 + 3)/30
1/v = 1/30
v = +30 cm
Result:
The image is formed at a distance of 30 cm behind the mirror.
Lens
1. An object is placed at a distance of 60 cm from a concave lens of focal length 30 cm. Use lens formula to find the position of the image formed in this case.
[CBSE 2025]
View Solution
Given:
Object distance, u = −60 cm
Focal length of concave lens, f = −30 cm
Lens formula:
1/f = 1/v + 1/u
Substituting the values:
1/(−30) = 1/v + 1/(−60)
−1/30 = 1/v − 1/60
1/v = −1/30 + 1/60
Taking LCM (60):
1/v = (−2 + 1)/60
1/v = −1/60
v = −60 cm
Result:
The image is formed at a distance of 60 cm in front of the lens.
2. Out of the two lenses, one concave and the other convex, state which one will diverge a parallel beam of light falling on it. Draw a ray diagram to show the principal focus of the lens.
[CBSE 2025]
View Solution
Identification:
Out of the two lenses, a concave lens diverges a parallel beam of light falling on it.
Explanation:
When a parallel beam of light passes through a concave lens, the rays spread out (diverge) after refraction. These diverging rays appear to come from a point on the principal axis called the principal focus of the concave lens.
Ray diagram (description):
A set of parallel rays incident on a concave lens diverges after refraction. When these refracted rays are produced backward, they meet at the principal focus on the same side of the lens as the object.
3. A ray of light after refraction from a convex lens emerges parallel to its principal axis.
(i) Draw a labelled ray diagram to show it.
(ii) In this case, the incident ray before refraction from the lens passes through a point on its principal axis. Name the point.
[CBSE 2025]
View Solution
(i) Ray diagram (description):
A ray of light incident on a convex lens passes through its principal focus on the object side. After refraction from the lens, the ray emerges parallel to the principal axis. The principal axis, optical centre, and principal focus are shown and labelled in the diagram.
(ii) Name of the point:
The incident ray passes through the principal focus (F) of the convex lens before refraction.
Refraction
1. Study the figure in which the path of a ray of light going from Medium 1 to Medium 2 is shown.
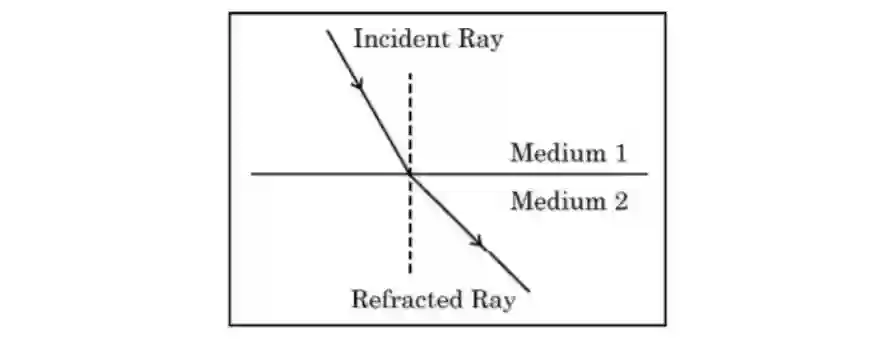
(a) Out of the two Media Medium 1 and Medium 2, in which is the speed of light more?
(b) State reason of bending of the refracted ray away from the normal.
(c) Express refractive index of Medium 2 with respect to Medium 1 in terms of speed of light in two media.
[CBSE 2025]
View Solution
(a) Medium in which speed of light is more:
The speed of light is more in Medium 1.
(b) Reason for bending of refracted ray away from the normal:
The refracted ray bends away from the normal because light is travelling from an optically denser medium (Medium 1) to an optically rarer medium (Medium 2). As a result, the speed of light increases in Medium 2.
(c) Refractive index of Medium 2 with respect to Medium 1:
The refractive index of Medium 2 with respect to Medium 1 is given by:
n21 = v1 / v2
where v1 is the speed of light in Medium 1 and v2 is the speed of light in Medium 2.
2. The values of absolute refractive indices of kerosene and water are 1.44 and 1.33 respectively. Compare the two media on the basis of their
(a) optical density
(b) mass density
(c) relative speed of propagation of light.
What do you infer on the basis of above comparisons?
[CBSE 2025]
View Solution
Given:
Absolute refractive index of kerosene, nk = 1.44
Absolute refractive index of water, nw = 1.33
(a) Optical density:
Optical density of a medium is directly proportional to its refractive index. Since 1.44 > 1.33, kerosene is optically denser than water.
(b) Mass density:
Mass density depends on the mass and volume of a substance and is not related to the refractive index. Therefore, no comparison of mass density can be made from the given data.
(c) Relative speed of propagation of light:
Speed of light in a medium is inversely proportional to its refractive index. Since the refractive index of water is less than that of kerosene, light travels faster in water than in kerosene.
Inference:
A medium with a higher refractive index is optically denser and allows light to travel more slowly. Optical density of a medium is independent of its mass density.
3. When an incident ray of light enters a medium ‘X’ from air, it bends towards the normal. Infer about the following with respect to air:
(a) Optical density of medium ‘X’.
(b) Speed of light through medium ‘X’Give reason for your answer in each case.
[CBSE 2025]
View Solution
(a) Optical density of medium X:
Medium X is optically denser than air.
Reason: A ray of light bends towards the normal when it travels from an optically rarer medium to an optically denser medium.
(b) Speed of light in medium X:
The speed of light in medium X is less than that in air.
Reason: In an optically denser medium, the speed of light decreases compared to an optically rarer medium like air.
Chapter 2. Human Eye
Human Eye
1. Name the type of lenses required by the persons for the correction of their defect of vision called presbyopia.
Write the structure of the lenses commonly used for the correction of this defect giving reason for such designs.
[CBSE 2025]
View Solution
Type of lens required:
Persons suffering from presbyopia require bifocal lenses for the correction of this defect of vision.
Structure of the lens and reason:
A bifocal lens consists of two parts:
- The upper part is a concave lens, which helps the person to see distant objects clearly.
- The lower part is a convex lens, which helps the person to see nearby objects clearly.
Reason: In presbyopia, the power of accommodation of the eye decreases due to weakening of eye muscles with age. Therefore, a combination of concave and convex lenses is used so that both distant and near objects can be seen clearly.
2. A student has difficulty in reading his textbooks but can read the blackboard clearly while sitting in the last row.
Name the defect of vision the student is suffering from.
List two reasons due to which this defect arises.
Write the nature of the lenses required to correct this defect.
[CBSE 2025]
View Solution
Name of the defect of vision:
The student is suffering from Hypermetropia (long-sightedness).
Reasons for this defect:
- The focal length of the eye lens increases due to weakening of the ciliary muscles.
- The eyeball becomes shorter than its normal length.
Nature of lens required for correction:
A convex lens of suitable power is used to correct hypermetropia.
Prism
1. Draw a ray diagram to show the path of a ray of light falling obliquely on one of the refracting faces of a triangular glass prism and mark the angle of deviation on it.
[CBSE 2025]
View Solution
Ray diagram (description):
A ray of light is incident obliquely on one refracting face of a triangular glass prism. The ray bends towards the normal on entering the prism due to refraction. Inside the prism, it travels towards the second refracting face and bends away from the normal on emerging into air.
The angle between the direction of the incident ray (produced forward) and the direction of the emergent ray is called the angle of deviation (δ). This angle is clearly marked outside the prism between the extended incident ray and the emergent ray.
Labels to be shown in the diagram:
Triangular glass prism
Incident ray
Refracted ray inside the prism
Emergent ray
Angle of deviation (δ)
2. Draw a ray diagram to show the refraction of a ray of light passing through an equilateral glass prism. Mark the angle through which the emergent ray bends from the direction of the incident ray and also name it.
[CBSE 2025]
View Solution
Ray diagram (description):
A ray of light is incident obliquely on one refracting face of an equilateral glass prism. On entering the prism, the ray bends towards the normal due to refraction. It then travels inside the prism and strikes the second refracting face, where it bends away from the normal and emerges into air as the emergent ray.
The angle between the direction of the incident ray (produced forward) and the direction of the emergent ray is clearly marked outside the prism.
Name of the angle:
The angle through which the emergent ray bends from the direction of the incident ray is called the angle of deviation (δ).
Labels to be shown in the diagram:
Equilateral glass prism
Incident ray
Refracted ray inside the prism
Emergent ray
Angle of deviation (δ)
Atmospheric Refraction
1. Give reasons:
(i) The sky appears dark to passengers flying at very high altitude.
(ii) ‘Danger’ signal lights are red in colour.
[CBSE 2025]
View Solution
(i) The sky appears dark to passengers flying at very high altitude:
At very high altitude, the density of air molecules is very low. Due to fewer air molecules, scattering of sunlight is negligible. Therefore, very little light is scattered and the sky appears dark.
(ii) ‘Danger’ signal lights are red in colour:
Red light has the longest wavelength and is scattered the least by air, fog, and smoke. Hence, red light can be seen from a long distance clearly, making it suitable for danger signal lights.
2. What is a rainbow? “We see a rainbow in the sky only after the rainfall.” Why?
[CBSE 2025]
View Solution
Rainbow:
A rainbow is a natural spectrum of seven colours formed in the sky due to the dispersion of sunlight by tiny water droplets present in the atmosphere.
Reason for seeing a rainbow only after rainfall:
After rainfall, numerous tiny water droplets remain suspended in the air. These water droplets act like small prisms and cause refraction, dispersion, and total internal reflection of sunlight, resulting in the formation of a rainbow.
Chapter 3. Electricity
Potential
1. Heat produced per second due to a current in a resistor of 4 Ω is 400 joules. Calculate the potential difference across the resistor.
[CBSE 2025]
View Solution
Given:
Resistance, R = 4 Ω
Heat produced per second = Power, P = 400 W
Formula used:
P = V² / R
Substituting the values:
400 = V² / 4
V² = 400 × 4
V² = 1600
V = 40 V
Result:
The potential difference across the resistor is 40 volts.
Ohm’s Law
1. A wire of resistance R is cut into three equal parts. If these three parts are then joined in parallel, calculate the total resistance of the combination so formed.
[CBSE 2025]
View Solution
Given:
Resistance of the original wire = R
Resistance of each part:
When a wire is cut into three equal parts, the length of each part becomes one-third. Since resistance is directly proportional to length,
Resistance of each part = R / 3
Combination of the three parts:
The three equal resistances (R/3) are connected in parallel.
Equivalent resistance in parallel:
1 / Req = 1/(R/3) + 1/(R/3) + 1/(R/3)
1 / Req = 3/R + 3/R + 3/R
1 / Req = 9 / R
Req = R / 9
Result:
The total resistance of the combination is R / 9.
2. Two lamps, rated 100 W; 220 V and 60 W; 220 V are connected in parallel to electric main supply of 220 V. Find the current drawn by the two lamps from the supply.
[CBSE 2025]
View Solution
Given:
Rating of first lamp: P₁ = 100 W, V = 220 V
Rating of second lamp: P₂ = 60 W, V = 220 V
Formula used:
I = P / V
Current drawn by 100 W lamp:
I₁ = 100 / 220 = 0.455 A
Current drawn by 60 W lamp:
I₂ = 60 / 220 = 0.273 A
Total current drawn from the supply:
I = I₁ + I₂
I = 0.455 + 0.273 = 0.728 A
Result:
The total current drawn by the two lamps from the supply is approximately 0.73 A.
3. Consider two lamps A and B of rating 50 W; 220 V and 25 W; 220 V respectively. Find the ratio of the resistances of the two lamps (i.e. RA : RB).
[CBSE 2025]
View Solution
Given:
Rating of lamp A: P₁ = 50 W, V = 220 V
Rating of lamp B: P₂ = 25 W, V = 220 V
Formula used:
R = V² / P
Resistance of lamp A:
RA = 220² / 50
Resistance of lamp B:
RB = 220² / 25
Ratio of resistances:
RA : RB = (220² / 50) : (220² / 25)
Cancelling common terms:
RA : RB = 25 : 50
RA : RB = 1 : 2
Combination of Resistors
1. Determine the total resistance of the parallel combination of three resistances of 2 Ω, 4 Ω and 6 Ω.
[CBSE 2025]
View Solution
Given:
Resistances: R₁ = 2 Ω, R₂ = 4 Ω, R₃ = 6 Ω
Formula used (parallel combination):
1 / Req = 1/R₁ + 1/R₂ + 1/R₃
Substituting the values:
1 / Req = 1/2 + 1/4 + 1/6
Taking LCM (12):
1 / Req = 6/12 + 3/12 + 2/12
1 / Req = 11 / 12
Req = 12 / 11 Ω
Result:
The total resistance of the parallel combination is 12/11 Ω (approximately 1.09 Ω).
2. Determine the maximum and minimum resistance which can be obtained by joining five resistors of 1/5 ohm each.
[CBSE 2025]
View Solution
Given:
Number of resistors = 5
Resistance of each resistor = 1/5 Ω
Maximum resistance:
Maximum resistance is obtained when all resistors are connected in series.
Rmax = 5 × (1/5)
Rmax = 1 Ω
Minimum resistance:
Minimum resistance is obtained when all resistors are connected in parallel.
1 / Rmin = 5 / (1/5)
1 / Rmin = 25
Rmin = 1 / 25 Ω
Result:
Maximum resistance = 1 Ω
Minimum resistance = 1/25 Ω
3. Four resistors, each of resistance 2 Ω, are joined end to end to form a square ABCD as shown. Using appropriate formula, determine the equivalent resistance of the combination between its two ends A and B.
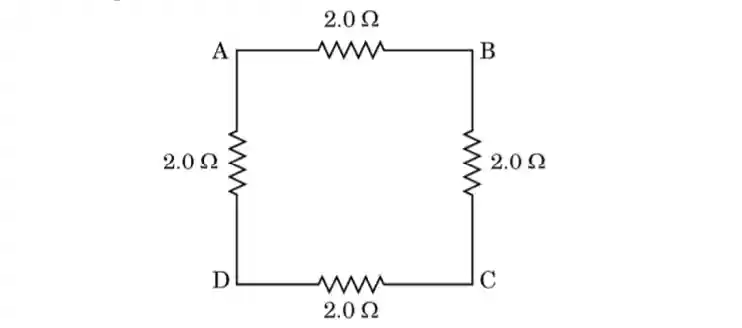
[CBSE 2025]
View Solution
Given:
Each resistor has resistance 2 Ω.
Understanding the circuit:
Between points A and B, there are two possible paths for current:
- Direct path AB having resistance 2 Ω
- Path A → D → C → B consisting of three resistors in series
Resistance of path A → D → C → B:
R = 2 + 2 + 2 = 6 Ω
Equivalent resistance between A and B:
The two paths (2 Ω and 6 Ω) are in parallel.
1 / Req = 1/2 + 1/6
1 / Req = (3 + 1) / 6
1 / Req = 4 / 6 = 2 / 3
Req = 3 / 2 Ω
Result:
The equivalent resistance between points A and B is 3/2 Ω (or 1.5 Ω).
4. Use Ohm’s law to determine the potential difference across the 6 Ω resistor in the following circuit when key is closed:
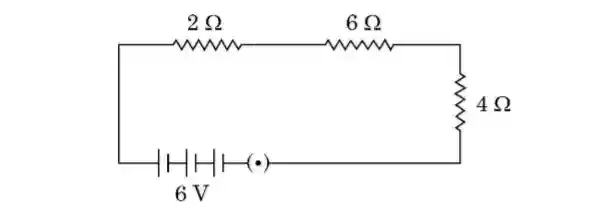
[CBSE 2025]
View Solution
Given:
Resistance values: 2 Ω, 6 Ω, 4 Ω
Battery voltage, V = 6 V
Total resistance of the circuit:
All resistors are connected in series.
R = 2 + 6 + 4 = 12 Ω
Current flowing in the circuit:
Using Ohm’s law,
I = V / R = 6 / 12 = 0.5 A
Potential difference across the 6 Ω resistor:
V = IR
V = 0.5 × 6 = 3 V
Result:
The potential difference across the 6 Ω resistor is 3 volts.
Power
1. Define electric power. When do we say that the power consumed in an electric circuit is 1 watt ?
[CBSE 2025]
View Solution
Electric power:
Electric power is the rate at which electrical energy is consumed or electrical work is done in an electric circuit.
Condition for 1 watt power:
The power consumed in an electric circuit is said to be 1 watt when 1 joule of electrical energy is consumed in 1 second.
2. Consider the following circuits :
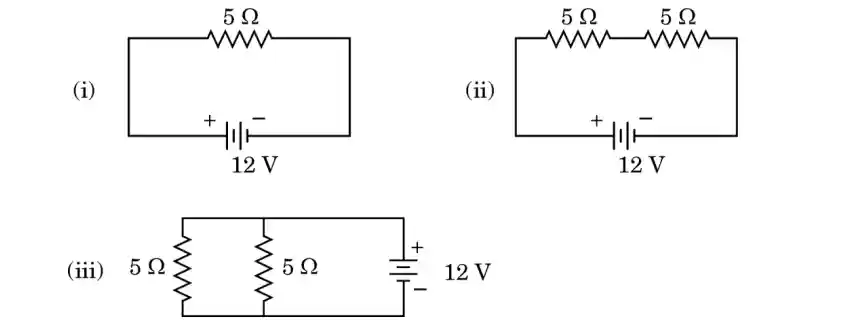
In which circuit will the power dissipated in the circuit be
(I) minimum (II) maximum ?
Justify your answer.
[CBSE 2025]
View Solution
Given:
Supply voltage in each circuit = 12 V
Power dissipated in a circuit is given by:
P = V² / R
Analysis of the circuits:
Circuit (i):
Single resistor of 5 Ω
Equivalent resistance, R₁ = 5 Ω
Circuit (ii):
Two resistors of 5 Ω each in series
R₂ = 5 + 5 = 10 Ω
Circuit (iii):
Two resistors of 5 Ω each in parallel
1 / R₃ = 1/5 + 1/5 = 2/5
R₃ = 5/2 = 2.5 Ω
Comparison of power:
Since P = V² / R, power is inversely proportional to resistance.
Maximum power:
Occurs in the circuit having minimum resistance, i.e. Circuit (iii).
Minimum power:
Occurs in the circuit having maximum resistance, i.e. Circuit (ii).
Result:
(I) Power dissipated is minimum in circuit (ii).
(II) Power dissipated is maximum in circuit (iii).
3. An electric kettle is rated 750 W; 220 V. Can this kettle be used in a circuit which has a fuse of current rating 3 A ? Give reason for your answer.
[CBSE 2025]
View Solution
Given:
Power of kettle, P = 750 W
Voltage, V = 220 V
Fuse rating = 3 A
Current drawn by the kettle:
Using the relation,
I = P / V
I = 750 / 220
I ≈ 3.41 A
Conclusion:
The kettle cannot be used in a circuit having a fuse of rating 3 A.
Reason:
The current drawn by the kettle (3.41 A) is greater than the fuse rating. Therefore, the fuse will melt and break the circuit.
4. An electric fuse is rated 8 A. Can it be used with an electrical appliance of rating 5 kW, 200 V ? Justify your answer.
[CBSE 2025]
View Solution
Given:
Power of appliance, P = 5 kW = 5000 W
Voltage, V = 200 V
Fuse rating = 8 A
Current drawn by the appliance:
Using the relation,
I = P / V
I = 5000 / 200
I = 25 A
Conclusion:
The fuse cannot be used with this electrical appliance.
Reason:
The current drawn by the appliance (25 A) is much greater than the fuse rating (8 A). Hence, the fuse will melt and break the circuit.
5. An electric kettle is rated 230 V; 1000 W. Calculate the resistance of its heating element when in operation.
[CBSE 2025]
View Solution
Given:
Voltage, V = 230 V
Power, P = 1000 W
Formula used:
R = V² / P
Substituting the values:
R = (230)² / 1000
R = 52900 / 1000
R = 52.9 Ω
Result:
The resistance of the heating element of the kettle is 52.9 Ω.
Energy
1. A voltage source sends a current of 2 A to a resistor of 40 Ω connected across it for 5 minutes. Calculate the electrical energy supplied by the source.
[CBSE 2025]
View Solution
Given:
Current, I = 2 A
Resistance, R = 40 Ω
Time, t = 5 minutes = 300 s
Formula used:
Electrical power, P = I²R
Electrical energy, E = Pt
Calculation of power:
P = (2)² × 40
P = 4 × 40 = 160 W
Calculation of electrical energy:
E = 160 × 300
E = 48000 J
Result:
The electrical energy supplied by the source is 48,000 joules.
2. State two applications of Joule’s heating in domestic electric circuit.
[CBSE 2025]
View Solution
Applications of Joule’s heating in domestic electric circuit:
It is used in an electric fuse, where excessive current produces heat and melts the fuse wire, thereby protecting the circuit.
It is used in electric heating appliances such as electric iron, heater, toaster, kettle, and geyser to produce heat.
3. Establish the relationship between the commercial unit of electric energy and the SI unit of electric energy.
[CBSE 2025]
View Solution
Commercial unit of electric energy:
The commercial unit of electric energy is kilowatt-hour (kWh).
SI unit of electric energy:
The SI unit of electric energy is joule (J).
Relationship between the two units:
1 kilowatt = 1000 watt
1 hour = 60 × 60 = 3600 seconds
1 kWh = 1000 W × 3600 s
1 kWh = 3.6 × 106 J
Result:
One unit of electrical energy (1 kWh) is equal to 3.6 × 106 joules.
4. Prove that if the current through a resistor is increased by 100%, then the increase in power dissipated through the resistor will be 300%.
[CBSE 2025]
View Solution
Let:
Initial current through the resistor = I
Resistance of the resistor = R
Initial power dissipated:
Power, P = I²R
P₁ = I²R
Increase in current:
Increase of current by 100% means the current becomes double.
New current, I₂ = 2I
New power dissipated:
P₂ = (2I)²R
P₂ = 4I²R
Increase in power:
Increase = P₂ − P₁
Increase = 4I²R − I²R = 3I²R
Percentage increase in power:
(Increase / Original power) × 100
= (3I²R / I²R) × 100
= 300%
Conclusion:
If the current through a resistor is increased by 100%, the power dissipated through the resistor increases by 300%.
5. Calculate potential difference across a 4 Ω resistor that produces 100 J of heat every second.
[CBSE 2025]
View Solution
Given:
Resistance, R = 4 Ω
Heat produced per second = Power, P = 100 W
Formula used:
P = V² / R
Substituting the values:
100 = V² / 4
V² = 400
V = 20 V
Result:
The potential difference across the resistor is 20 volts.
Chapter 4. Magnetic Effect Of Electric Current
Domestic Electric Circuit
1. State the role of an electric fuse, used in series with an electrical appliance. Why should in an electric circuit a fuse with defined rating not be replaced by one with a larger rating?
[CBSE 2025]
View Solution
Role of an electric fuse:
An electric fuse is a safety device used in series with an electrical appliance to protect the circuit from excessive current. When the current exceeds the safe limit, the fuse wire heats up and melts, thereby breaking the circuit and preventing damage to the appliance.
Reason for not using a fuse of larger rating:
A fuse with a larger current rating will not melt when excessive current flows through the circuit. As a result, the circuit will remain closed, which may cause overheating, damage to appliances, or even fire hazards. Therefore, a fuse of proper defined rating must always be used.
2. How and why is an electric fuse used in an electric circuit ? Briefly describe its function.
[CBSE 2025]
View Solution
Use of an electric fuse:
An electric fuse is connected in series with an electric circuit to protect electrical appliances from damage due to excessive current.
Why it is used:
When excessive current flows through the circuit due to overloading or short circuit, the fuse wire gets heated and melts, thereby breaking the circuit.
Function of an electric fuse:
The fuse prevents overheating of wires and protects electrical appliances by stopping the flow of current when it exceeds the safe limit, thus reducing the risk of fire.
Yes, 2 marks questions are frequently asked in CBSE exams and are mostly concept-based. Practicing PYQs helps students understand the exam pattern.
Yes, all solutions are prepared strictly according to the CBSE 2024–25 syllabus and marking scheme.
Yes, regular practice of previous year questions improves accuracy, speed, and confidence in board exams.