3.1 Introduction
3.2 Scalars and vectors
3.3 Multiplication of vectors by real numbers
3.4 Addition and subtraction of vectors — graphical method
3.5 Resolution of vectors
3.6 Vector addition — analytical] method
3.7 Motion in a plane
3.8 Motion in a plane with constant acceleration
3.9 Projectile motion
3.10 Uniform circular motion
Table of Contents
- Vector
- Scalars and vectors
- Graphical Representation of Vectors
- Angle Between Two Vector
- Types of Vectors
- Addition and subtraction of vectors — graphical method
- Mathematical Representation of Vector
- Magnitude of Vector
- Resolution of Vectors
- Rectangular Components of a Vector
- Multiplication or division of a vector by a Scalar
- Scalar or dot Product of two Vectors
- Cross or Vector Product of Two Vectors
- Right hand thumb rule
- Motion in a Plane
- Position and Displacement Vectors in Two Dimensions
- Velocity
- Acceleration
- Motion in a Plane with Constant Acceleration
- Projectile Motion
- Projectile Projected Horizontally from a Height
- Projectile Projected at an angle with Horizontal
- Uniform Circular Motion
- Angular Displacement
- Angular Velocity
- Time Period
- Frequency
- Relation between Linear velocity and angular velocity
- Angular Acceleration
- Centripetal Acceleration
- Tangential Acceleration
- Radial Acceleration
Physical Quantity: Quantity that can be measure is called physical quantity.
Ex. Mass, Velocity , Density, Volume, Temperature.
Non- Physical Quantity: Quantity that can not be measure is called non-physical quantity.
Ex. Love, hate, goodness , light, sound, inertia
Scalar Quantity: A physical quantity which can be described completely by its magnitude only and does not require a direction is known as a scalar quantity. It obey the ordinary rules of algebra.
Ex. Distance , Mass, Time, Speed , Temperature etc.
Vector Quantity: A physical quantity which requires magnitude and a particular direction, when it is expressed, is known as vector quantity.
Ex. Displacement, Velocity, Acceleration, Force, Momentum
Vector
A quantity that has magnitude and direction and that is commonly represented by a directed line segment whose length represents the magnitude and whose orientation in space represents the direction.
Graphical Representation of Vectors
A vector is represented by a directed line segment.
- Length of the arrow represents the magnitude of the vector.
- Arrowhead shows the direction of the vector.
Note : Vector can be shifted parallel to itself keeping its magnitude and direction same.
Note : Rotation of vector other than (θ=2π =360 ) is not allowed.
Angle Between Two Vector
The smaller angle between two vectors when they are placed head-to-head or tail-to-tail is called the angle between the vectors.
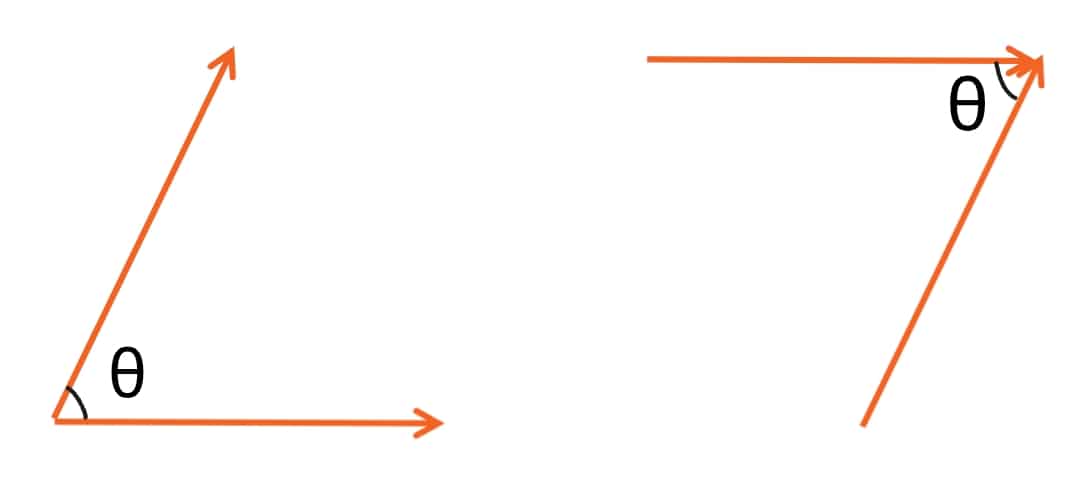
Note: If angle between vector \overrightarrow{A} and \overrightarrow{B} is θ then angle between \overrightarrow{A} and -\overrightarrow{B} is 180-θ and -\overrightarrow{A} and -\overrightarrow{B} is θ.
Question: A vector is not changed if
(A) it is rotated through an arbitrary angle
(B) it is multiplied by an arbitrary scalar
(C) it is cross multiplied by a unite vector.
(D) it is slid parallel to itself ✓
Types of Vectors
Equal Vector: Those vectors which are of the same nature, have the same magnitude, and act in the same direction are called equal vectors.
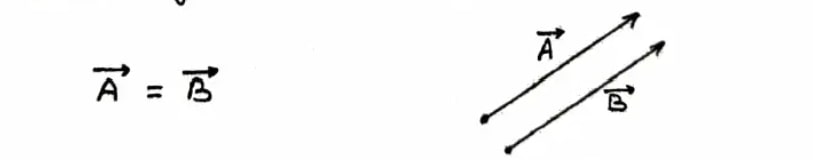
Opposite Vector (Negative Vector ): Those vectors which are of the same nature, have equal magnitude but act in exactly opposite directions are called opposite vectors (or negative vectors).
Parallel Vector: Magnitude may or may not equal, but direction must be same.
Note : All equal vectors are parallel.
Note : All parallel vector may or may not equal vector.
Anti-Parallel Vector : Magnitude may or may not equal but direction opposite.
Note : All negative vectors are anti- parallel.
Note : All anti-parallel may or may not be negative of each other.
Zero Vector (Null Vector) : A vector having zero magnitude.
Ex. Velocity of a car which is at rest.
Note : Sum of equal and opposite vectors is null vector.
Collinear Vector: All vector are called colinear when they are along the same line.
Co-planer Vector : Those vectors which are in same plane is called co-planer vectors.
Orthogonal Vector (Perpendicular Vector ) : Those vectors which are at right angle (90°) to each other are called orthogonal vectors.
Note : Magnitude may or may not same but angle must be 90°.
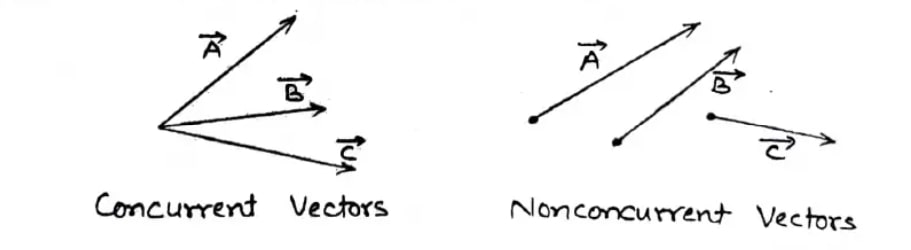
Concurrent Vector : Those vectors which act on the same point (common point of application) are called concurrent vectors.
Note: Magnitude and direction may or may not be same but point of action is at same point.
Axial Vector: Those vectors which represent rotational effect and act along the axis of rotation are called axial vectors
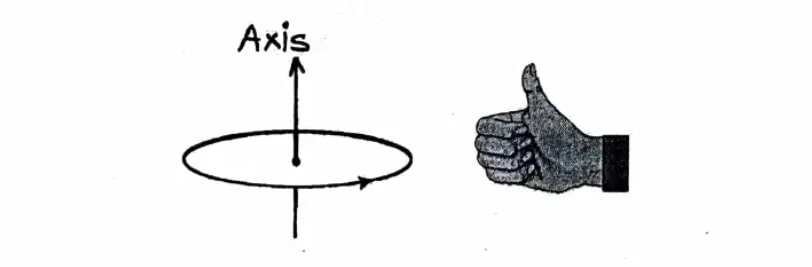
Ex. Torque, Angular Velocity, Angular Acceleration, Angular Momentum.
Polar Vector : Those vectors which have a starting point (initial point) and represent linear motion or displacement are called polar vectors.
Note: Polar vectors are also known as true vectors.
Ex. Displacement, Velocity, Acceleration, Force, Electric field etc.
Unit Vector: A vector whose magnitude is equal to 1 unit is called a unit vector.
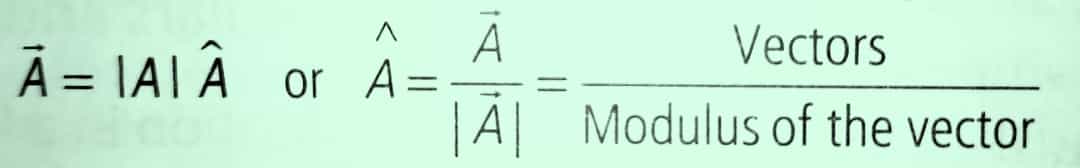
Note: Unit vector represent only direction.
Note: Unit vector is unitless and dimensionsless.
Question : True – False
- All equal vector must be parallel.
- All parallel vector must be equal.
- All anti parallel are -ve of each other.
- Two parallel vector may be -ve of each other.
- All colinear are parallel vector.
- All parallel vectors are colinear.
Answer: 1. True, 2. False, 3. False, 4. False, 5. False, 6. True
Question : Assertion: A null vector is a vector whose magnitude is zero and direction is arbitrary.
Reason: A null vector does not exist.
- Both A and R are true and reason is the correct explanation of assertion.
- Both A and R are true but reason is not the correct explanation of assertion.
- Assertion is true but reason is false ✓
- Both assertion and reason are false.
Addition and subtraction of vectors — graphical method
A. Geometrical Method
Geometrical method of addition of vector helps us in understanding the vectors and the resultant vectors. This method contains three laws.
1. Triangle Law of Vector Addition
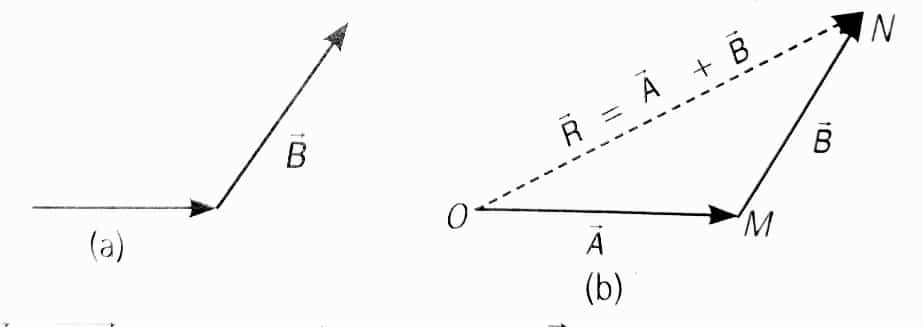
If two non-zero vectors are represented by the two sides of a triangle taken in same order then the resultant is given by the third side of triangle in opposite order.
2. Parallelogram Law of Vector Addition
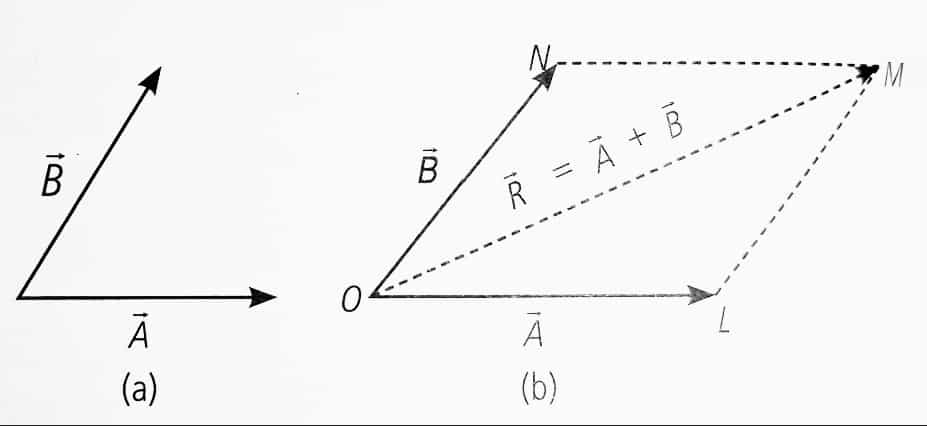
If two non-zero vector are represented by the two adjacent sides of a parallelogram then the resultant is given by the diagonal of the parallelogram passing through the point of intersection of the two vectors.
3. Polygon Law of vectors Addition
If several vectors are placed one after another (head to tail) to form a polygon, then the resultant vector is given by the side that closes the polygon, taken in the opposite direction.
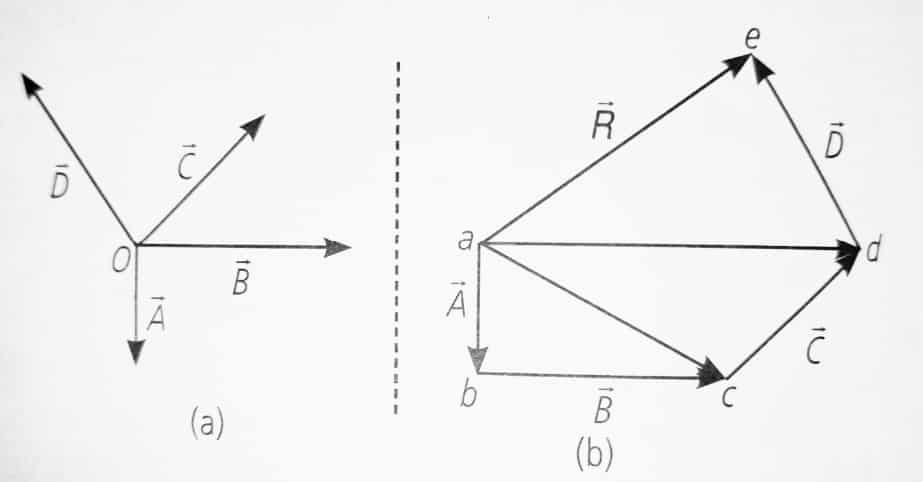
Note: In a polygon if all the vectors are in same order then their resultant is a null vector.
B. Vector Addition – Analytical Method
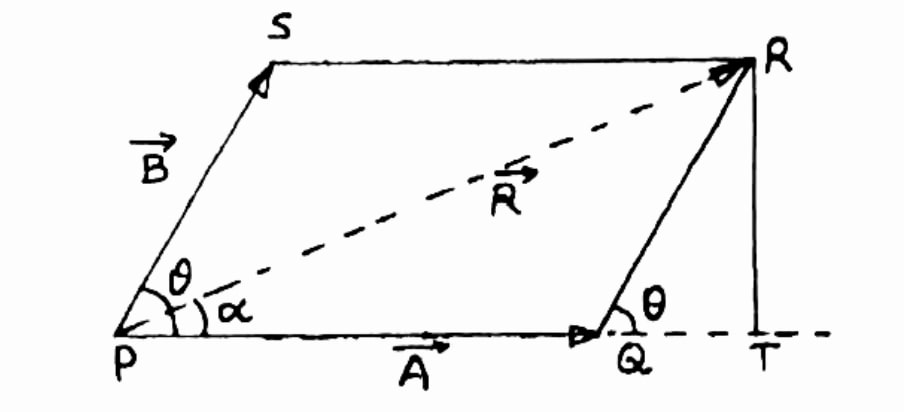
Question . Two vectors of 10 units and 5 units make an angle of 120° with each other. Find the magnitude and angle of resultant with vector of 10 unit magnitude.
Important Points
- (i) Resultant of two vectors will be maximum when they are parallel. i e. angel (θ) between them is zero.
- (ii) Resultant of two vectors will be minimum when they are antiparallel. i e. angel (θ) between them is 180°.
- (iii) Vector addition is commutative.
- (Iv) Vector addition is associative.
- (v) Resultant of two vectors of equal magnitude will be at their bisector.
- (vi) If vectors are of unequal magnitude then minimum three coplanar vectors are required for zero resultant.
- (viii) If vectors are of unequal magnitude and non coplanar then then minimum four vectors are required for zero resultant.
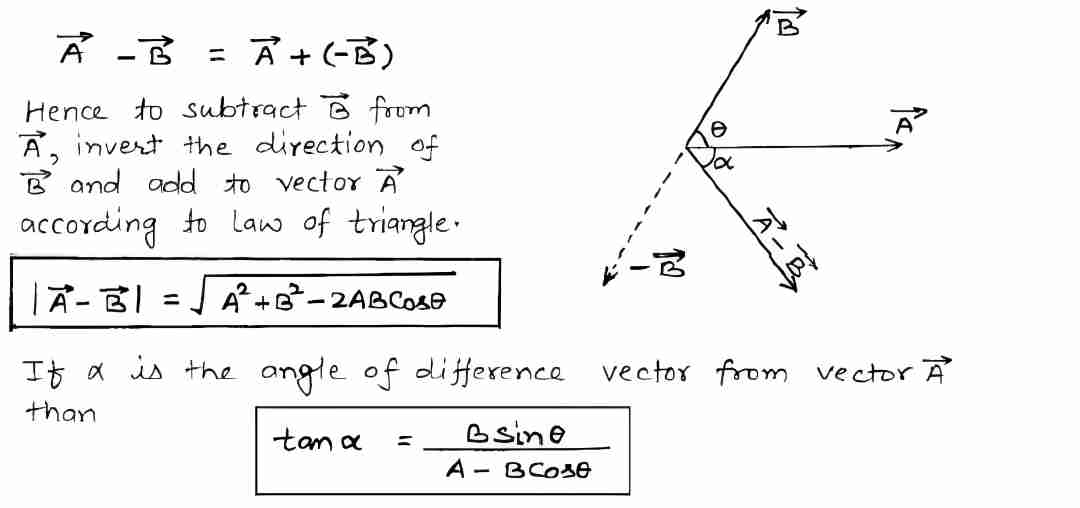
Subtraction of two vectors
Let \vec{A} and \vec{B} are two vectors. Their difference i.e. \vec{A}– \vec{B} can be treated as sum of the vector \vec{A} and vector \vec{(-B)}.
Mathematical Representation of Vector
A vector is mathematically represented by a quantity that has both magnitude and direction. It is usually written in bold letter or with an arrow above the letter.
For example, a vector A is written as: \overrightarrow{A}
In Cartesian (3D) coordinate system, a vector is represented as:
\overrightarrow{A}=A_{x}\overset{∧}{i}+A_{y}\overset{∧}{j}+A_{z}\overset{∧}{k}
Components of Vector
The components of a vector are the projections of the vector along the coordinate axes. They help us to express the vector in terms of its effects in each direction (like x-axis, y-axis, and z-axis).
In 3D, a vector is written as:
\vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}where, Ax, Ay, and Az are the components along x, y, and z axes.
Note: In 2D, if a vector A makes an angle θ with the x-axis, then it is written as:
\vec{A} = A_x \hat{i} + A_y \hat{j}where,
- A_x = A \cos \theta
- A_y = A \sin \theta
Magnitude of Vector
The magnitude of a vector (also called the length or absolute value) is a scalar quantity that represents how long or strong the vector is, without considering its direction. It is denoted by placing vertical bars around the vector symbol, like this: |\vec{A}|
The magnitude of the vector can be written as:
|\vec{A}| = \sqrt{A_x^2 + A_y^2 + A_z^2}